Inflation. High interest rates. Crypto collapses. Bah humbug. How about we forget about the economy for this digest? Let’s take a more festive perspective. Here are a couple of maps about Santa!
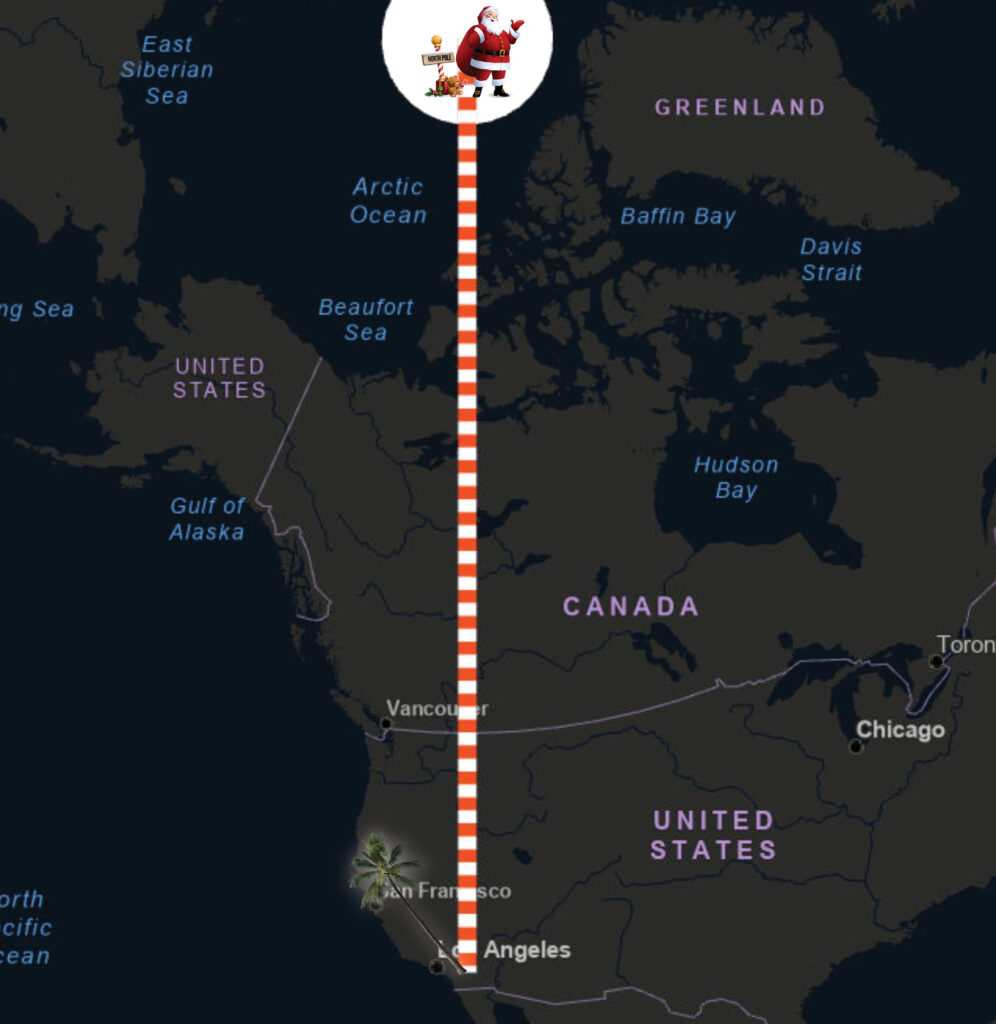
So how long is Santa’s trip from the North Pole to the Coachella Valley? This introduces the cartographer’s dilemma. How do we, with the least distortion, draw our 3-dimensional spherical planet in two dimensions? By making a lot of compromises. We do this by “projecting” the sphere onto a flat medium (e.g., paper or flat computer screens). When we do this we immediately set in distortions that intensify as we move away from the center of the map. Just imagine flattening an orange peel. The peel rips and warps as you flatten it. It is not a pretty sight.
This first map uses a projection that does the best it can to retain the shape of map elements like countries. We’ve made a choice. So accuracy in the other critical cartographic characteristics: area, distance, and direction, is sacrificed. If we measure Santa’s trip from this map we get 3,741 miles.
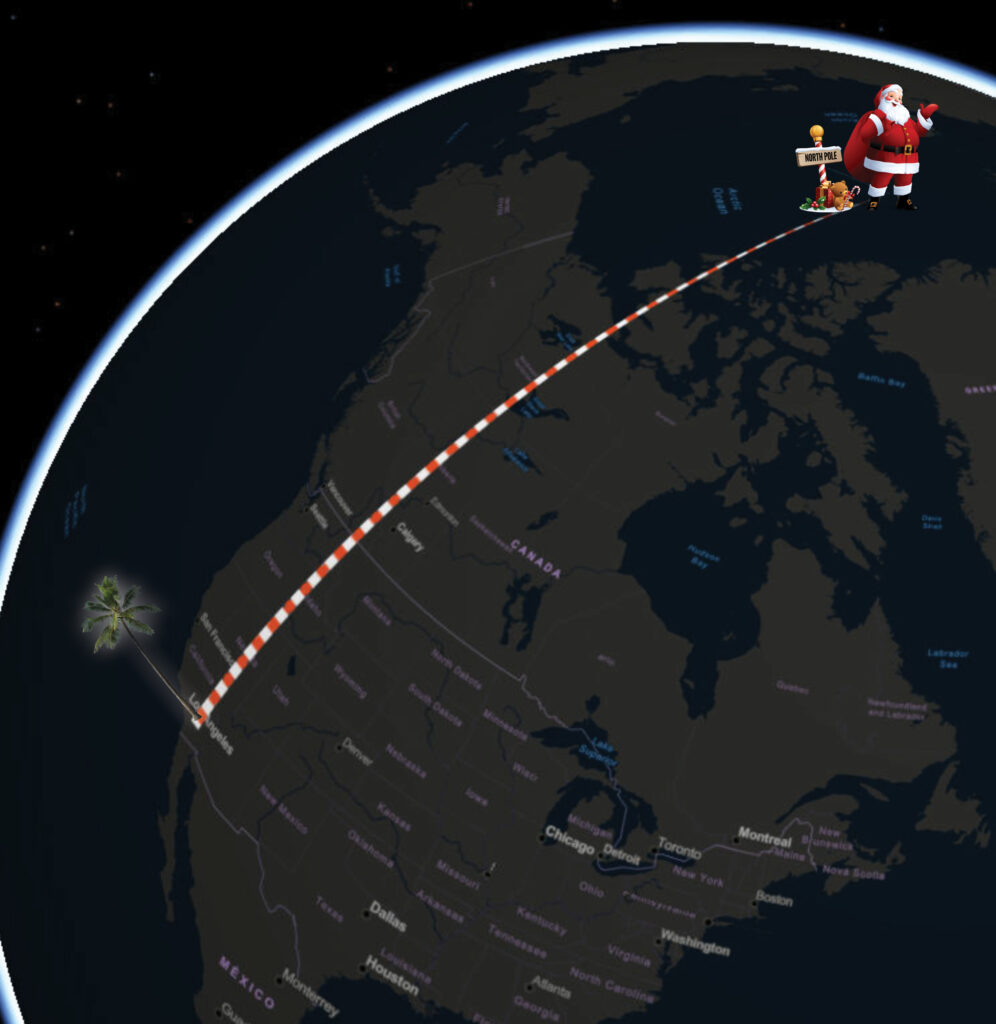This map is a picture of a three-dimensional spherical representation of our map like one would see using an app like Google Earth. Here the distance is 3,895 miles. Why the additional 154 miles? Because we are taking into consideration the curvature of the earth. It’s as if you placed a string on a globe between two places holding it close to the curved surface. You then pull it off the globe while still holding the two points, and flatten it. That would be the true distance. Santa and his reindeer surely know these calculations in order to logistically pull off their one-night navigational feat.
Happy Holidays everyone!
